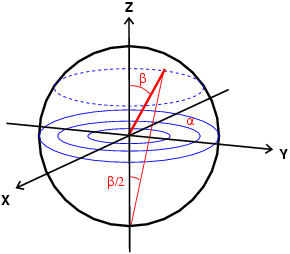
PoleFigures
< Define the compression direction | Radial Diffraction | Data Coverage In Axial Diffraction Experiments >
Using pole figures to represent directions in space
Dealing with textures and orientations, pole figures become really usefull tools to represent orientations, when you understand what they mean! The two figures below briefly explain how to relate the directions in space to pole figures.
The exact relation between the angles alpha and beta and distances on the pole figure plot depends on the type of projection you use. Most common are the sterographic projection and the equal area projection.
In the stereographic projection (Wulff net), the distance between the center and the point is proportional to tan(beta/2). In the equal area projection (Schmidt net), the distance between the center and the point is proportional to sin(beta/2).
 |  |
| Figure 1: Directions in space can be represented by two angles, which I labelled alpha and beta in the figure above. There are many conventions for the names and the extact definition of those angles in texture studies, so be careful! | Figure 2: Projection on a pole figure. Projection on pole figures are used to map directions in 3-D space onto a plane. Y direction in the figure on the right corresponds to A0, X is at A6, Z is at C1 and the direction in red somewhere near B2. |
In experiments performed in compression, the direction of compression usually serves as reference for the Z axis, therefore, we always plot things as a function of their orientation to this direction of compression, Z, which should always be at the center of the pole figure.