PolycrystalVelocitiesInMTex
Plotting seismic velocities in MTex
Let's say you ran a VPSC calculation and you want to plot the resulting texture and corresponding seismic velocities. MTex can do all of it a few clicks. Here is how...
Set up Mtex
Startup Matlab, start Mtex. Usually, I change the original projections to have X to the east, Y to the North, and Z in the center. This is what I am used to. Here are the corresponding commands:
% Start Mtex startup_mtex % Put X to the left of the projection (convention I use, Mtex puts x to the North by default) plotx2east; % Check where the X-axis is plot(xvector,'Marker','p','MarkerSize',15,'MarkerFaceColor','red','MarkerEdgeColor','black')
Mtex will plot something like this, telling you were the X direction is
Plot of the X direction in MTex (after setting
plotx2east)Load a check you texture
Before loading the texture, you should set your sample and crystal symmetries. In the current example, I will work with a polycrystal olivine (orthorhombic) and no special sample symmetry. I then load a VPSC texture from 60_SO_oli.tex
% Set crystal and sample symmetry
cs = symmetry('orthorhombic',[ 4.7346, 10.2149, 5.9902])
ss = symmetry('-1');
% Load the VPSC texture file
halfwidth = 10*degree;
fname = fullfile('/path/to/texture/','','60_SO_oli.tex');
ebsd60 = loadEBSD_generic(fname,'cs',cs,'ss',ss,'bunge','degree','ColumnNames',{'Euler 1' 'Euler 2' 'Euler 3' 'weight'},'header',4,'Columns',[1,2,3,4]);
You can download this texture file for testing from this link 60_SO_oli.tex.
It corresponds to the texture in a polycrystal of olivine at 60 km depth, according to the calculations presented in
Convert the texture to an ODF and plot 100 and 001 pole figures
% Create an ODF and plot a 100 and 001 pole figure, for checking
odf = calcODF(ebsd60)
plotpdf(odf,[Miller(1,0,0),Miller(0,0,1)],'contourf', 'antipodal','gray')
setcolorrange('equal');
colorbar
You should get something like this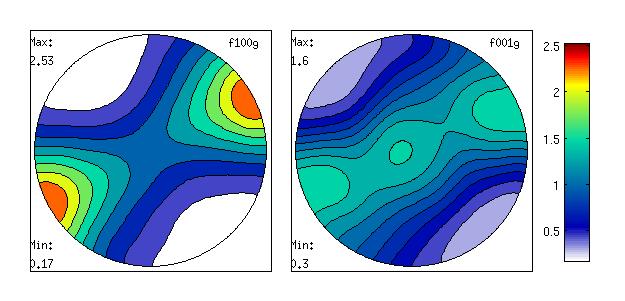
100 and 001 pole figures for our olivine polycrystal
Calculating seismic velocities
Now, we want to calculate seismic velocities for our polycrystal. You need to end the single crystal elastic moduli, density, and calculate the corresponding elastic tensor for the polycrystal. Here is how to do
% Create single crystal elastic tensor, P = 1.97 GPa, T = 1444 K Olivine_Mat60 = ... [[287 64 67 0.0 0.0 0.0];... [ 64 173 74 0.0 0.0 0.0];... [ 77 74 205 0.0 0.0 0.0];... [ 0.0 0.0 0.0 52 0.0 0.0];... [ 0.0 0.0 0.0 0.0 66 0.0];... [ 0.0 0.0 0.0 0.0 0.0 65]]; Cij60 = tensor(Olivine_Mat60,'name','elastic stiffness','unit','GPa', cs); % Provide density rho60 = 3.21 % Calculate elastic averages for the polycrystal [ Tvoigt60 , Treuss60 , Thill60 ] = calcTensor(ebsd60, Cij60)
This will generate 3 tensors, Tvoigt60, Treuss60, and Thill60 with the elastic properties of the polycrystal in the Voigt, Reuss, and Hill average.
Plotting compression wave velocities
Here is an example for plotting compression wave velocities
plot (Thill60,'PlotType' , 'velocity' , 'vp' , 'complete', 'density' , rho60 )
axis off
box off
colorbar
title('Vp (km/s) - 60 km')
You will get a figure like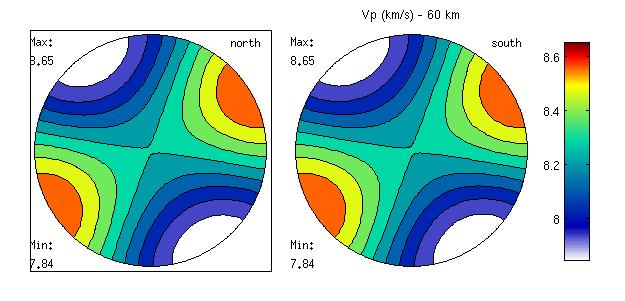
Compression wave velocities for our olivine polycrystal
If, for some reason, you want to fix the contours yourself, this is how you do
plot (Thill60,'PlotType' , 'velocity' , 'vp' , 'complete', 'density' , rho60, 'colorRange', [7.75 8.75], 'contours', [7.75 7.95 8.15 8.35 8.55 8.75] )
axis off
box off
colorbar
title('Vp (km/s) - 60 km - 0.2 km/s contour')
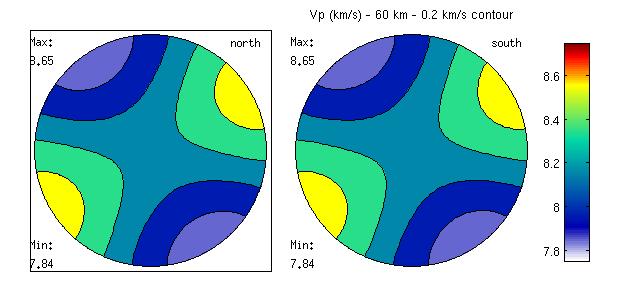Compression wave velocities for our olivine polycrystal, with contours every 0.2 km/s
Plotting shear wave anisotropy
If you want to plot the shear wave anisotropy, in percent, use
plot (Thill60,'PlotType' , 'velocity' , '200*(vs1-vs2)./(vs1+vs2)' , 'density' , rho60 )
axis off
box off
colorbar
title('dVs (%) - 60 km')
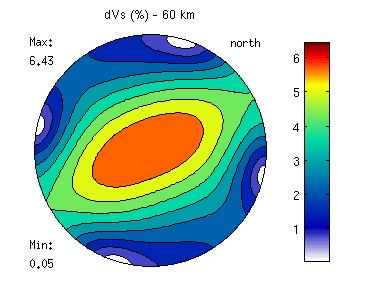Shear wave anisotropy for our olivine polycrystal
If, for some reason, you want to fix the contours yourself, this is how you do
plot (Thill60,'PlotType' , 'velocity' , '200*(vs1-vs2)./(vs1+vs2)' , 'density' , rho60, 'colorRange', [0 7], 'contours', [0 1 2 3 4 5 6 7] )
axis off
box off
colorbar
title('dVs (%) - 60 km - contours 1%')
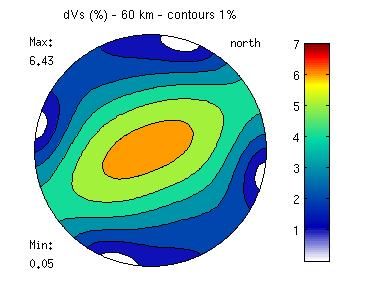Shear wave anisotropy with fixed contours for our olivine polycrystal
Plotting shear wave anisotropy, along with the direction of polarization of the fast shear wave
If you want to plot the shear wave anisotropy, along with the direction of polarization of the fast shear wave, you should use
plot (Thill60,'PlotType' , 'velocity' , '200*(vs1-vs2)./(vs1+vs2)' , 'density' , rho60)
hold all
plot (Thill60,'PlotType' , 'velocity' , 'ps1' , 'density' , rho60, 'LineWidth',2 )
hold off
box off
axis off
colorbar
title('dVs (%) - 60 km')
And here is the result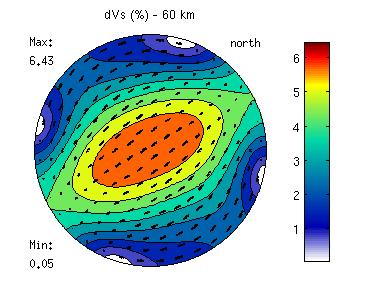
Shear wave anisotropy along with the direction of the fast polarization for our olivine polycrystal