
 Next: Mesure expérimentale des constantes
Up: Élasticité sous pression
Previous: Rapide introduction à l'élasticité
Subsections
Next: Mesure expérimentale des constantes
Up: Élasticité sous pression
Previous: Rapide introduction à l'élasticité
Subsections
Pour déduire les propriétés polycristallines du matériau considéré, il faut
moyenner les modules élastiques pour déduire les modules d'incompressibilité
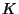
et de
cisaillement
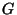
qui sont directement reliés au vitesse de propagation d'ondes.
On utilise différentes hypothèses
- l'hypothèse de Voigt: on suppose la continuité des déformations, c'est à
dire que les grains s'emboitent parfaitement mais que des discontinuités de contraintes
peuvent apparaître aux interfaces.
- l'hypothèse de Reuss: on suppose la continuité des contraintes, c'est à dire
que les contraintes sont uniformes à travers l'aggrégat mais que les grains ne
s'emboitent pas parfaitement.
- l'hypothèse de Hill: on utilise une simple moyenne arithmétique des quantités
calculées dans le cas Reuss et Voigt,
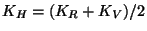 et
et
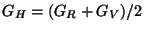 .
.
L'expérience montre que les résultats numériques obtenus par l'hypothèse de Hill
ne sont généralement pas trop éloignées des valeurs expérimentales. Il existe
de nombreuses autres méthodes pour calculer ces quantités qui sont détaillées dans
les ouvrages ou publications spécialisées.
L'élasticité d'un cristal cubique est caractérisée par
3 modules indépendants:
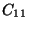
,
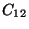
et
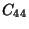
.
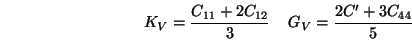 |
(8) |
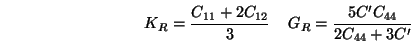 |
(9) |
 |
(10) |
L'élasticité d'un cristal hexagonal est caractérisée par
5 modules indépendants:
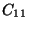
,
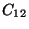
,
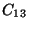
,
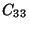
et
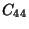
.
![\begin{displaymath}
K_V= {1 \over 9} \left[ 2(C_{11}+C_{12}) +C_{33} + 4 C_{13} \right] \;\;\;\;
G_V= {1 \over 30}(M + 12 C_{44} + 12 C_{66})
\end{displaymath}](img30.png) |
(11) |
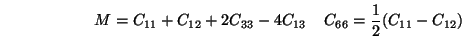 |
(12) |
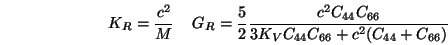 |
(13) |
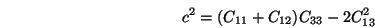 |
(14) |
L'élasticité d'un cristal trigonal est caractérisée par
6 modules indépendants:
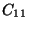
,
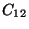
,
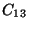
,
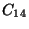
,
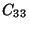
et
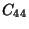
.
![\begin{displaymath}
K_V= {1 \over 9} \left[ 2(C_{11}+C_{12}) +C_{33} + 4 C_{13} \right] \;\;\;\;
G_V= {1 \over 30}(M + 12 C_{44} + 12 C_{66})
\end{displaymath}](img30.png) |
(15) |
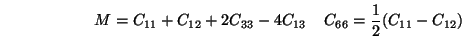 |
(16) |
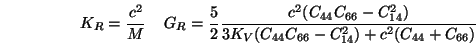 |
(17) |
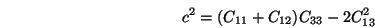 |
(18) |
L'élasticité d'un cristal tétragonal est caractérisée par
6 modules indépendants:
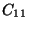
,
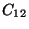
,
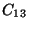
,
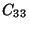
,
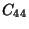
et
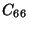
.
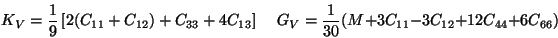 |
(19) |
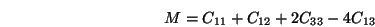 |
(20) |
![\begin{displaymath}
K_R = {c^2 \over M} \;\;\;\;
G_R = 15 \left[ 18 {K_V \over c...
...11}-C_{12}} + {6 \over C_{44}} + {3 \over C_{66}} \right]^{-1}
\end{displaymath}](img39.png) |
(21) |
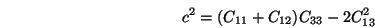 |
(22) |

 Next: Mesure expérimentale des constantes
Up: Élasticité sous pression
Previous: Rapide introduction à l'élasticité
Sebastien Merkel
2002-02-06
Next: Mesure expérimentale des constantes
Up: Élasticité sous pression
Previous: Rapide introduction à l'élasticité
Sebastien Merkel
2002-02-06
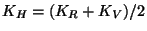 et
et
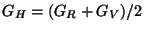 .
.

