Next: Méthodes expérimentales Up: La diffraction de rayons X Previous: La diffraction de rayons X
Introduction à la diffraction de rayons X
Dans une expérience de diffraction de rayons X,
l'échantillon peut être un solide monocristallin,
polycristallin ou bien encore une poudre. Il est placé
dans une enceinte appropriée puis illuminé par une
source collimatée ou focalisée. Les photons X
diffusés de manière élastiques seront collectés
par un détecteur avec une intensité maximale pour
les plans cristallins en incidence de Bragg
où
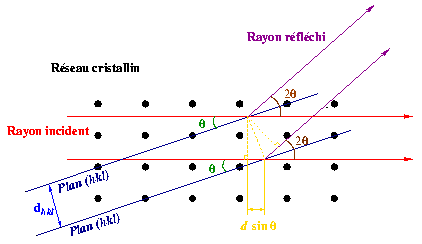
| Condition de Bragg pour des plans cristallins d'indice de Miller (hkl) et de distance inter-réiculaire dhkl. La difféence de marche entre les photons X réfléhis par des plans successifs correspond à un multiple de la longueur d'onde du faisceau incident. |
La loi de Bragg est donc une conséquence de la périodicité
du réseau cristallin. Une réflection de Bragg
n'est possible que si
![]() .
Pour un cristal usuel, 2d est de l'ordre de
quelques angrströms, donc lambda doit être
aussi de l'ordre de quelques angrströms, ce qui
correspond au domaines des rayons X.
.
Pour un cristal usuel, 2d est de l'ordre de
quelques angrströms, donc lambda doit être
aussi de l'ordre de quelques angrströms, ce qui
correspond au domaines des rayons X.
Next: Méthodes expérimentales Up: La diffraction de rayons X Previous: La diffraction de rayons X Sebastien Merkel
2000-09-29

