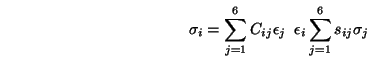
 Next: Propriétés des polycristaux
Up: Élasticité sous pression
Previous: Élasticité sous pression
Subsections
Next: Propriétés des polycristaux
Up: Élasticité sous pression
Previous: Élasticité sous pression
Subsections
Les tenseurs des contraintes dans un cristal sont représentés par les matrices
suivantes:
![\begin{displaymath}
\left[\epsilon\right] = \left[\begin{array}{ccc}
\epsilon_{...
...\
\sigma_{31} & \sigma_{32} & \sigma_{33}
\end{array}\right]
\end{displaymath}](img1.png) |
(1) |
Si l'on reste en deca d'une certaine limite , la
limite élastique, les déformations subies par un cristal
sont réversibles. De plus, pour de faibles déformations, on
constate que la quantité de déformation est proportionnelle
aux contraintes appliquées.
Au niveau microscopique cela implique que le tenseur des déformations d'un cristal
peut être reliées au tenseur des contrainte par une loi linéaire
(
loi de Hook). On définit ainsi un tenseur du deuxième ordre
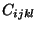
où
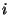
,
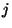
,
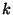
et
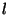
varient de 1 à 3 tel que
 |
(2) |
ou encore
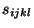
où
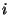
,
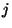
,
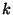
et
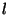
varient de 1 à 3 tel que
 |
(3) |
Les
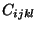
sont les modules élastiques (souvent appelés constantes
élastiques, mais ils ne sont pas constants...) et les
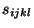
coefficients de déformabilité.
Les symétries des tenseurs
de contrainte et de déformations font qu'on se ramène généralement
à une matrice 6x6 (
notation de Voigt):
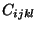
et
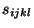
deviennent
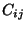
et
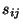
par la transformation des indices suivante:
| Tenseur |
11 |
22 |
33 |
23 |
32 |
13 |
31 |
12 |
21 |
| Matrice |
1 |
2 |
3 |
4 |
4 |
5 |
5 |
6 |
6 |
Le tenseur des contraintes devient un vecteur
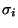
tel que
![\begin{displaymath}
\left[\sigma\right] = \left[\begin{array}{ccc}
\sigma_{11} ...
...\\
\sigma_{5} & \sigma_{4} & \sigma_{3}
\end{array}\right]
\end{displaymath}](img13.png) |
(4) |
Le tenseur des déformations devient un vecteur.
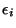
tel que
![\begin{displaymath}
\left[\epsilon\right] = \left[\begin{array}{ccc}
\epsilon_{...
...} & \frac{1}{2}\epsilon_{4} & \epsilon_{3}
\end{array}\right]
\end{displaymath}](img15.png) |
(5) |
On a
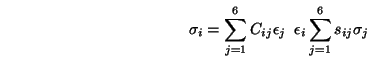 |
(6) |
et
 |
(7) |
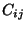
et
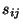
ont 36 coefficients indépendants. Des considérations sur le travail
et l'énergie permettent de ramener ce nombre à 21 (ces matrices est symétrique).
Puis la symétrie du cristal diminue encore le nombre de paramètres indépendants.
| symétrie |
Nombre de composantes indépendantes |
| cubique |
3 |
| hexagonale |
5 |
| tetragonale |
6 |
| trigonale |
6 ou 7 |
| orthorombique |
9 |
| monoclinique |
13 |
| triclinique |
21 |

 Next: Propriétés des polycristaux
Up: Élasticité sous pression
Previous: Élasticité sous pression
Sebastien Merkel
2002-02-06
Next: Propriétés des polycristaux
Up: Élasticité sous pression
Previous: Élasticité sous pression
Sebastien Merkel
2002-02-06
![\begin{displaymath}
\left[\epsilon\right] = \left[\begin{array}{ccc}
\epsilon_{...
...\
\sigma_{31} & \sigma_{32} & \sigma_{33}
\end{array}\right]
\end{displaymath}](img1.png)


![\begin{displaymath}
\left[\sigma\right] = \left[\begin{array}{ccc}
\sigma_{11} ...
...\\
\sigma_{5} & \sigma_{4} & \sigma_{3}
\end{array}\right]
\end{displaymath}](img13.png)
![\begin{displaymath}
\left[\epsilon\right] = \left[\begin{array}{ccc}
\epsilon_{...
...} & \frac{1}{2}\epsilon_{4} & \epsilon_{3}
\end{array}\right]
\end{displaymath}](img15.png)